Science

Three Equations of Motion

Posted on by HelpYouBetter

The equations that relate displacement (S), time taken (t), initial velocity (u), final velocity (v) and uniform acceleration (a) are called equations of motion.

Consider an object moving along a straight line with a uniform acceleration ‘a’. The motion can be described in terms of the following three kinematic relations:

First Equation of Motion: Velocity – Time Relation

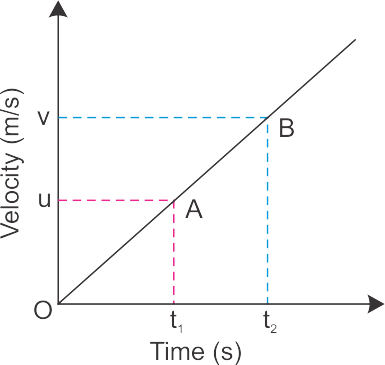
First Equation of Motion: Velocity – Time Relation

Figure 1

Consider a particle moving along a straight line with a constant acceleration ‘a’. Let the velocity of the particle be v0 at time t = 0, and after a time interval t, let the velocity be vt. Then, the acceleration of the particle is given by,large begin{aligned} a &=frac{v_{t}-v_{0}}{t} \ie.,;;;;; at&=v_{t}-v_{0} \or,;;;;;; v_{t} &=v_{0}+at ;;;;;-------(1)end{aligned}

If the velocity of the particle at t = 0  is represented by u the initial velocity, and that at the instant t is represented by v the final velocity, then,large begin{aligned} ;;;;;; v &=u+at ;;;;;-------(2)end{aligned}

This is the velocity-time relation for uniformly accelerated motion.

Second Equation of Motion: Position – Time Relation

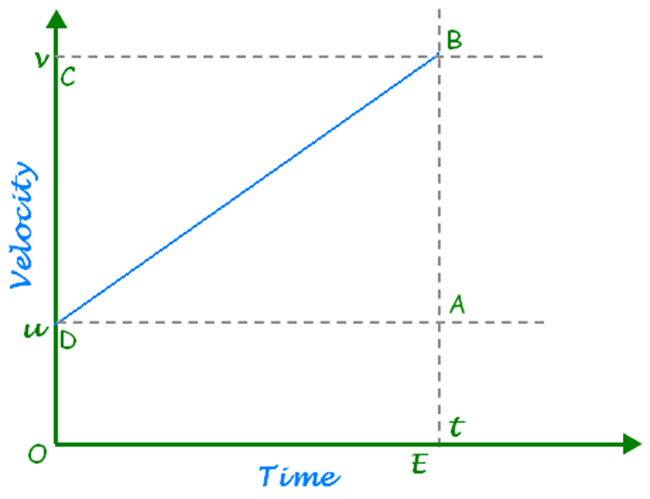
Second Equation of Motion Position – Time Relation

Figure 2

Consider an object moving along a straight  line with constant acceleration ‘a’. Let the velocity of the object be v0 and the position co-ordinate be x0 at time t = 0. Similarly, after a time interval t, let the velocity of the object be vt and the position co-ordinate be xt . Now (xt – x0 ) is called the displacement ‘s’ of the object during this interval of time and large begin{aligned} frac{v_{0}+v_{t}}{2} end{aligned}is the average velocity. Then, begin{aligned} Displacement&=Average;velocitytimes time \ie.,;;;;;;;;x_{t}-x_{0}&=left ( frac{v_{0}+v_{t}}{2} right )(t-0) \&=left ( frac{v_{0}+v_{t}}{2} right )t \Substituting;the;&equation;for;v_{t};from;equation;(7),;we;get, \x_{t}-x_{0}&=left ( frac{v_{0}+v_{0}+at}{2} right )t \&=left ( frac{2v_{0}+at}{2} right )t \&=left ( frac{2v_{0}}{2}+frac{at}{2} right )t \&=left (v_{0}+frac{at^{2}}{2}right )t \ie.,;;;;;;;;x_{t}-x_{0}&=;;v_{0}t+frac{1}{2}at^{2} \The;position;co-&ordinate;x_{t};of;the;object;at;time;t;is;given;by, \x_{t}&=x_{0}+v_{0}t+frac{1}{2}at^{2};;;;;-------(3) \The;displacement;&(x_{t}-x_{0});is;represented;by;s,then, \s&=v_{0}t+frac{1}{2}at^{2};;;;;;;;;;;;;-------(4) \If;velocity;v_{0};at;t=0&;is;replaced;by;u,;the;initial;velocity;then;equation;(4);becomes, \s&=ut+frac{1}{2}at^{2};;;;;;;;;;;;;;;-------(5) end{aligned}

In equation (3), the first term gives the displacement of the object at t = 0, the second term gives the displacement contribution due to the velocity in the absence of acceleration and the third term gives the displacement contribution due to acceleration. Since the third term of the equation contains t2,  the position time graph of the motion of the object will be parabolic in shape as shown in figure 3(a). Similarly, if the object is moving with a deceleration the position time graph will be as shown in figure 3(b).

Figure 3

Third Equation of Motion: Position – Velocity Relation

Figure 4

Consider an object moving along a straight line with constant acceleration ‘a’. Let the velocity of the object be v0 and the position co-ordinate be x0 at time t = 0. Similarly, after a time interval t, let the velocity of the object be vt and the position co-ordinate be xt .large begin{aligned} Then;by;eqn(1),;;;;v_{t}&=v_{0}+at \Squaring;both;sides,;;;(v_{t})^{2}&=(v_{0}+at)^{2} \ie.,;;;;v_{t}^{2}&=v_{0}^{2}+2v_{0}at+a^{2}t^{2} \&=v_{0}^{2}+ 2aleft [ v_{0}t+frac{1}{2}at^{2} right ] \By;eqn(4),left [v_{0}t+frac{1}{2}at^{2}right ]=s,;&the;displacement;during;the;time;interval;t. \therefore ;we;get,;;;;;;;;;v_{t}^{2}&=v_{0}^{2}+2as;;;;;;;;;;;;;-------(6) \or,;;;;;;;;;;v_{t}^{2}&=v_{0}^{2}+2a(x_{t}-x_{0}) \If;v_{0};is;replaced;by;u;the;init&ial;velocity;and;v_{t};by;the;final;velocity;v,;above;eqn;(6);becomes, \v^{2}&=u^{2}+2as;;;;;;;;;;;;;-------(7) end{aligned}

Thus the equations (2), (5) and (7) represent the most general forms of equations of motion of an object moving along a straight line with constant acceleration.

Distance covered by a particle in the nth second of motion

The displacement of a body in the nth second of motion can be calculated as follows:

Let s and s’ be the displacement of the object having an initial velocity v0 and an acceleration ‘a’ at time, t = n and t = (n-1) seconds respectively. Then,large begin{aligned} s&=v_{0}n+frac{1}{2}an^{2} \and;;;;;;;s'&=v_{0}(n-1)+frac{1}{2}a(n-1)^{2} \therefore;displacement;in;the;n^{th};second,;;;;;S_{n}&=s-s' \&=v_{0}n+frac{1}{2}an^{2}-(v_{0}(n-1)+frac{1}{2}a(n-1)^{2}) \&=v_{0}n+frac{1}{2}an^{2}-v_{0}(n-1)-frac{1}{2}a(n-1)^{2} \&=v_{0}n+frac{1}{2}an^{2}-v_{0}(n-1)-frac{1}{2}a(n^{2}-2n+1) \&=v_{0}n+frac{1}{2}an^{2}-v_{0}n+v_{0}-frac{1}{2}an^{2}+an-frac{1}{2}a \&=v_{0}+an-frac{1}{2}a \&=v_{0}+frac{1}{2}a(2n-1);;;;;;;;;;;;;-------(8) \If;v_{0};is;replaced;by;the;initial;velocity;&u,;equation;(8);becomes, \S_{n}&=u+frac{1}{2}a(2n-1);;;;;;;;;;;;;;-------(9) end{aligned}

Vertical motion under gravity

Galileo proved through his feather and coin experiment that all bodies irrespective of their mass, reach the ground at the same time. That is, all particles near the surface of the earth experience the force of gravity and this force produces the same acceleration on all particles irrespective of their masses. The acceleration thus produced is called the acceleration due to gravity (g) and is always directed towards the centre of the earth. The value of acceleration due to gravity (g), on or, near the surface of earth is about 9.8 m/s2.

When a body falls freely, its equations of motion are obtained by replacing acceleration(a) in the above equations by the acceleration due to gravity(g), and displacement(s) by the height of the fall(h).

Thus, for downward motion, the equations becomes,large begin{aligned} \v&=u+gt;;;;;;;;;;;;;;;;;;;;;;-------(10) \h&=ut+frac{1}{2}gt^{2};;;;;;;;;;;;;;;;;-------(11) \v^{2}&=u^{2}+2gh;;;;;;;;;;;;;;;;;;-------(12) \h_{n}&=u+frac{1}{2}g(2n-1);;;;;;;;;-------(13) end{aligned}

Similarly, the equations of motion of a particle moving vertically upwards is obtained by replaing a by –g.

Thus, for upward motion, the equations becomes,large begin{aligned} \v&=u-gt;;;;;;;;;;;;;;;;;;;;;;-------(14) \h&=ut-frac{1}{2}gt^{2};;;;;;;;;;;;;;;;;-------(15) \v^{2}&=u^{2}-2gh;;;;;;;;;;;;;;;;;;-------(16) \h_{n}&=u-frac{1}{2}g(2n-1);;;;;;;;;-------(17) end{aligned}

In general, for motion under gravity, the acceleration always remains the same. That is, large begin{aligned} overrightarrow{a}=overrightarrow{g} end{aligned}. It is applicable for both upward and downward motion.

Equations of Motion Formulas

The concepts, formulas and derivations for the kinematic equations of motion with uniform acceleration are explained in this article. Let’s write the formulas of three equations of motion in the tabular form, which is necessary for solving the problems related to the equations of motion.

Equations of Motion

Formula
1st equation of motion large v = u + at
2nd equation of motion large s=ut+frac{1}{2}at^{2}
3rd equation of motion large v^{2}=u^{2}+2as
Distance covered in nth second of motion large S_{n}=u+frac{1}{2}a(2n-1)

Stay tuned with Helpyoubetter for the workout examples and problems related to the equations of motion. To learn more related articles, check the table mentioned below.

RELATED ARTICLES
Define acceleration and what are the different types of acceleration? What do you mean by the relative velocity of an object with respect to another?
Distinguish between speed and velocity. Explain the significance of the position-time graph for a body in uniform motion.
Explain the different types of errors occurring in the measurement of a physical quantity. Distinguish between the distance covered by a body and its displacement.
Rate this post
HelpYouBetter

HelpYouBetter is a blog, where the science-related topics are explained in a detailed and simpler way

Leave a Reply

Your email address will not be published. Required fields are marked *